RangeDependenciesAnalysed
From APIDesign
(→No Longer NP-Complete) |
(→No Longer NP-Complete) |
||
| Line 75: | Line 75: | ||
When '''compiling a module <math>A</math>''' with direct dependencies on <math>M^1_{[l_1,u_1)}, ..., M^n_{[l_n,u_n)}</math>. We can assume that <math>M^1_{l_1}, ..., M^n_{l_n}</math> exist and have all their transitive dependencies explicitly enumerated and are consistent (otherwise they could not be part of the ''complete repository''). Let's now collect all transitive dependencies of <math>M^1_{l_1}, ..., M^n_{l_n}</math> into a set <math>D</math> and verify whether they are all consistent. | When '''compiling a module <math>A</math>''' with direct dependencies on <math>M^1_{[l_1,u_1)}, ..., M^n_{[l_n,u_n)}</math>. We can assume that <math>M^1_{l_1}, ..., M^n_{l_n}</math> exist and have all their transitive dependencies explicitly enumerated and are consistent (otherwise they could not be part of the ''complete repository''). Let's now collect all transitive dependencies of <math>M^1_{l_1}, ..., M^n_{l_n}</math> into a set <math>D</math> and verify whether they are all consistent. | ||
| - | Compute the common denominator range for each module B: <math>cr = \cup { range : (\exist M) M \rightarrow B_{range} \in D }</math>, if: | + | Compute the common denominator range for each module B: <math>cr = \cup \{ range : (\exist M) M \rightarrow B_{range} \in D \}</math>, if: |
# <math>cr = \emptyset</math>, then reject the merge, as there is no version of module B that could satisfy all dependencies | # <math>cr = \emptyset</math>, then reject the merge, as there is no version of module B that could satisfy all dependencies | ||
# otherwise use <math>B_{cr}</math> as the range dependency on B | # otherwise use <math>B_{cr}</math> as the range dependency on B | ||
Obviously this kind of computation can be done in polynomial time. Thus we can perform this check during every compilation. When we have new configuration, we just need to seek the repository and find out if for each module in the configuration we have an existing version of the module that we can compile against. If such version is found, it will be used as a ''lower bound'' for the newly compiled module. The ''upper bound'' will be the inferred one, unless the compiled module restricts it. | Obviously this kind of computation can be done in polynomial time. Thus we can perform this check during every compilation. When we have new configuration, we just need to seek the repository and find out if for each module in the configuration we have an existing version of the module that we can compile against. If such version is found, it will be used as a ''lower bound'' for the newly compiled module. The ''upper bound'' will be the inferred one, unless the compiled module restricts it. | ||
Revision as of 13:57, 8 January 2012
When analysing dependencies it can be easily proven that RangeDependencies (as used by OSGi) are too flexible and may lead to NP-Complete problems. However recently I started to ask following question - it is known that LibraryReExportIsNPComplete and that the problem can be fixed by generating so called complete repositories. Can't the same trick be applied to repositories using RangeDependencies as well?
My current feeling is that it can. This page is my attempt to formalize the feeling to something more formal.
Contents |
Lower Bound
Each dependency has a lower bound, a minimal required version of a library that we can work against. When producing our application, it is in our interest to verify that we can really compile and create our application against the lower bound. The easiest way to ensure we are using only classes and methods available in such lower bound version is to compile against the lower bound version of each library we define a dependency on.
Or from the opposite perspective: Compiling against newer version than the lower bound is too errorprone. NetBeans allows this and especially during development cycle, when things are changing rapidly, this often leads to LinkageErrors that render the whole application unusable at random and unexpected moments.
Lower bound is the version that we compile against.
Upper bound
Upper bound on the other hand is the version that we know we can still work with.
There are just two vague verbs in the previous sentence. What does it mean to know?
- Know can mean to be sure. E.g. we have verified that we really work with that version. We have downloaded that version of a library, executed all our tests and certified it. We really checked our application works with that version. In some situations this kind of knowledge is required.
- Know can however mean to believe. Often we can trust the producer of the library, that they will conform to some versioning scheme (like Semantic versioning) and based on such trust we can estimate the upper bound.
What does it mean to work?
- Work can mean really runs as expected and this kind of verification is hard, tough to automate. It requires work of a quality department and is more a process decision than something scientifically definable.
- Work can be reduced to links, this is definitely much less satisfying answer (but at least it prevents the linkage errors, so it gives the application a chance to recover), but it is easily measurable. BinaryCompatibility can be verified by tools like Sigtest.
In case we want to believe our application will sort of work and for sure at least link to new version, it is better to use predefined, widely accepted RangeDependencies - e.g. when using a library with lower bound 1.5, the upper bound would automatically be 2.0. The range would be [1.5,2.0).
If one wants to be sure application really runs as expected, it is wiser to specify narrow range. If version 1.5 is the newest version, one can even use [1.5,1.5] and only when new versions are released, release new versions of the application and expand the range to [1.5,1.6].
The latter, paranoiac approach, is likely to be used more often in end user applications. The first, optimistic one, seems more suitable for reusable libraries.
Stability of Published API
How one specifies how stable just published API is? The semantic versioning suggests to treat all releases up to changed major version (e.g. up to 2.0.0) as being BinaryCompatible. The NetBeans API Stability proposal allows each API to be attributed as stable, devel or private. The netbeans:NbmPackageStability goes even further and suggests to use different ranges for different stability of the API. Is this the right approach?
In ideal, rationalistic world, it is. Under the assumption that API designers are rationalistic and understand the versioning issues and the importance of proper dependency management, it is fine to expect that they will do everything to follow principles of semantic versioning (or netbeans:NbmPackageStability guidelines) and either keep BackwardCompatibility or bump the major version. In rationalistic world, it is enough to believe our application will sort of work and at least link and the rest will be achieved by the good work of the other, rationalistic people.
The trouble is that we live in clueless world and most of the people (including API designers) don't have time to fully evaluate negative influence of their changes. When producers of up-stream library make a mistake, there should be a way for the consumers of such API to recover and shield themselves. From this thought there is just a small step to the idea of giving the users of an API right to classify stability of the API they use.
Should there be a repository of modules and their dependencies including module M in versions 1.1,1.2,1.5,2.0,2.5,3.0. If majority of other modules having a dependency on M uses range [1.1,2.0) (e.g. the classical range for semantic versioning), then we can deduce that the owner of module M is doing good job keeping BackwardCompatibility. If many dependencies on M use for example [1.1,1.5), then we can deduce that something unnatural (from the point of semantic versioning happened in version 1.5) and that the owner of the module M underestimated the impact of changes in version 1.5. On the other hand, if many dependencies on M use range like [1.1,3.0) then the incompatible change was probably not as incompatible as it might have seen.
The beauty of analysing the overall dependencies on a module is that it clearly expresses the statistical probability of BackwardCompatibility as seen by all users. It also allows the users to be sure application really runs as expected if the dependency is satisfied. Of course, the author of such API should set the expectations up by using stability category, but the ultimate decision remains in the hands of the API users.
Getting trapped by NP-Completeness
From the things described so far it seems that RangeDependencies may not be as bad, but still, there are severe NP-Complete problems associated with them. Following sections demonstrate the problems.
Module Repository with Ranges
Let A,B,C,... denote various modules and their APIs.
Let A1.0,A1.1,A1.7,A1.11,A2.1,A2.9,A3.0 denote versions of module A. It is not really important what format the versions use, the only condition is that there is a linear order among the versions. As such the rest of the terminology is using single variable (x or p) to denote the version.
Let 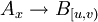 denote the fact that version x of module A depends on version range [u,v) of module B. E.g. any version of module B between u and less than v can be used to satisfy A's need. Let
denote the fact that version x of module A depends on version range [u,v) of module B. E.g. any version of module B between u and less than v can be used to satisfy A's need. Let ![A_{x} \rightarrow B_{[u,v]}](/images/math/8/8/7/8872c3ff5bd1572ca5aa11d2051404b6.png) denote closed interval dependency and allow its usage as well.
denote closed interval dependency and allow its usage as well.
Let Repository R = (M,D) be any set of modules with their versions and their dependencies on other modules.
Let C be a Configuration in a repository R = (M,D), if
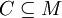 , where following is satisfied:
, where following is satisfied:
- each dependency is satisfied with some version from dependency range:
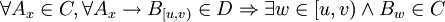
- only one version is enabled:
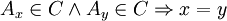
Module Range Dependency Problem
Let there be a repository R = (M,D) and a module 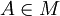 . Does there exist a configuration C in the repository R, such that the module
. Does there exist a configuration C in the repository R, such that the module 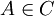 , e.g. the module can be enabled?
, e.g. the module can be enabled?
Conversion of 3SAT to Module Range Dependencies Problem
Let there be 3SAT formula with variables v1,...,vm as defined at in the original proof.
Let's create a repository of modules R. For each variable vi let's create two modules 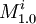 and
and 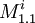 , and put them into repository R.
, and put them into repository R.
For each formula
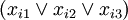 let's create a module Fi that will have three versions. Each of them will depend on one variable's module. In case the variable is used with negation, it will depend on version 1.0, otherwise on version 1.1. So for formula
let's create a module Fi that will have three versions. Each of them will depend on one variable's module. In case the variable is used with negation, it will depend on version 1.0, otherwise on version 1.1. So for formula
we will get:
All these modules and dependencies are added into repository R
Now we will create a module T1.0 that depends on all formulas:
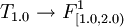
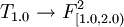
- ...
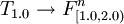
and add this module as well as its dependencies into repository R.
Claim: There 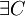 (a configuration) of repository R and
(a configuration) of repository R and 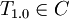
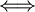 there is a solution to the 3SAT formula.
there is a solution to the 3SAT formula.
The proof is step by step similar to the one given in LibraryReExportIsNPComplete, so it is not necessary to repeat it here.
Avoiding NP-Completeness
Still RangeDependencies seem powerful. If we could eliminate the NP-Complete problems associated with them! If we could effectively find out whether dependencies of a module can be satisfied! Following lines show a way to do it.
Complete Module Repository with Ranges
A repository R = (M,D) is said to be complete if the transitive dependencies are explicitly enumerated:
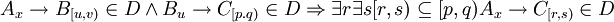
This definition seems to make sense from the point of lower bound. When module A is being compiled, it can request higher version of a library C then any of its dependencies require. In some cases A may need to use some new API available in C, so the ability to rise the lower bound seems reasonable.
It does not make much sense to have higher upper bound of dependency on C higher than any existing upper bound on C among reused libraries (thus s < = q). The module A may however be incapable to work with the whole range of versions of C that its dependencies can. Thus A can restrict upper bound (e.g. make s < q).
No Longer NP-Complete
Following the steps of first attempt to extinguish NP-completeness the time comes to demonstrate that complete range module repositories avoid NP-Completeness (under the assumption P!=NP) and that they can naturally be generated and verified for consistency.
First of all, the above conversion of 3SAT problem to module range repository cannot be used for complete module range repository. The central part of the conversion relies on the fact that module T1.0 has only indirect dependencies on Mi modules. Complete repositories prevent that.
The repository has to be populated incrementally by compiling new and new modules. Let's use this to demonstrate the construction of complete range repositories is possible in polynomial time:
module without dependencies - in almost any system there is at least one base module that does not have any dependencies. Computing set of dependencies of such module during compilation is obviously a constant operation.
When compiling a module A with direct dependencies on 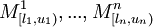 . We can assume that
. We can assume that 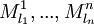 exist and have all their transitive dependencies explicitly enumerated and are consistent (otherwise they could not be part of the complete repository). Let's now collect all transitive dependencies of
exist and have all their transitive dependencies explicitly enumerated and are consistent (otherwise they could not be part of the complete repository). Let's now collect all transitive dependencies of 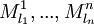 into a set D and verify whether they are all consistent.
into a set D and verify whether they are all consistent.
Compute the common denominator range for each module B: 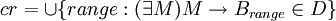 , if:
, if:
-
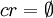 , then reject the merge, as there is no version of module B that could satisfy all dependencies
, then reject the merge, as there is no version of module B that could satisfy all dependencies
- otherwise use Bcr as the range dependency on B
Obviously this kind of computation can be done in polynomial time. Thus we can perform this check during every compilation. When we have new configuration, we just need to seek the repository and find out if for each module in the configuration we have an existing version of the module that we can compile against. If such version is found, it will be used as a lower bound for the newly compiled module. The upper bound will be the inferred one, unless the compiled module restricts it.
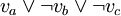
![F^i_{1.1} \rightarrow M^a_{[1.1,1.1]}](/images/math/a/5/8/a584d7505fc6f1ac104f585b6f939fc4.png)
![F^i_{1.2} \rightarrow M^b_{[1.0,1.0]}](/images/math/f/b/1/fb10a802c2c4b5c7a8e91bfcee01d16b.png)
![F^i_{1.3} \rightarrow M^c_{[1.0,1.0]}](/images/math/7/7/e/77ec15dd9f535101b63bf3294b5721b4.png)

