RangeDependencies

From APIDesign

(Difference between revisions)
Jump to: navigation, search
(→Too Much Flexibility will Kill You!)
(→Too Much Flexibility will Kill You!)
Line 10: Line 10:
==== [[wikipedia::Too_Much_Love_Will_Kill_You|Too Much Flexibility will Kill You]]! ====
==== [[wikipedia::Too_Much_Love_Will_Kill_You|Too Much Flexibility will Kill You]]! ====
-
Well, it seems that [[OSGi]] comrades made a mistake by choosing [[RangeDependencies]]. They created something that is flexible, as flexible that it is no longer manageable. Not only when one starts to deal with [[TransitivityOfIncompatibleChange]], but even in regular situations.
+
Although it may seem flexible, improperly using [[RangeDependencies]] may lead to system that is too complex and almost no longer manageable. What traditionally happens only when people release incompatible versions (due to [[TransitivityOfIncompatibleChange]]) can suddenly happen in regular situations.
The [[LibraryReExportIsNPComplete|proof]] claiming that managing module [[dependencies]] is [[NP-Complete]] operates with three types of modules:
The [[LibraryReExportIsNPComplete|proof]] claiming that managing module [[dependencies]] is [[NP-Complete]] operates with three types of modules:
Line 26: Line 26:
# single module <math>T</math> continue to depend on classical range of <math>F^j \in [1.0, 2.0)</math>
# single module <math>T</math> continue to depend on classical range of <math>F^j \in [1.0, 2.0)</math>
-
This is scenario following accepted practices of [[DistributedDevelopment]]. There is one team providing various versions of module <math>M^i</math> and that teams does its best to keep [[BackwardCompatibility]]. Its versioning follows the traditional way to denote compatible versions - e.g. the first ''major'' number stays the same, the second ''minor'' one is incremented.
+
This scenario describes accepted practices of [[DistributedDevelopment]]. Imagine, there is one team providing various versions of module <math>M^i</math>. This team does its best to keep [[BackwardCompatibility]]. It is using versioning in the traditional way to denote compatible versions - e.g. the first ''major'' number stays the same, the second ''minor'' one is incremented with each new, compatible version.
-
Yet there is some other distant team producing module(s) <math>F^j</math> and this team (or his quality department) is afraid of ''signing black checks'' and trusting the ''M''-team to produce compatible versions. Thus they use restricted [[RangeDependency]] to require just subset of the versions (only those known during testing).
+
Yet there is some other distant team producing module(s) <math>F^j</math> and this team (or its quality department) is afraid of ''signing blank checks'' and trusting the ''M''-team to produce compatible versions. Thus they use restricted [[RangeDependency]] to require just subset of the versions (only those known during testing).
-
This is all that needs to happen. No incompatibilities, just a simple use of [[RangeDependencies]] and we now facing an [[NP-Complete]] problem.
+
This is all that needs to happen. No incompatibilities, just a simple use of [[RangeDependencies]] and we are now facing an [[NP-Complete]] problem. This probably explains why there is [[3SAT]] solver behind [[Equinox]]. Finding the right setup of modules depending on each other with [[RangeDependencies]] can be really hard. [[NP-Complete]]ly hard.

Revision as of 19:45, 18 October 2009

Dependencies are important part of every Module system. Dependencies are here to abstract the complex relationship between a module and environment it needs for its own execution, compilation, linkage, etc. Dependencies are always a simplification of the real requirements, but that does not stop people from inventing new and new ways how to specify them more precisely.

It has already been discussed that dependency needs some lower bound (the moment when the needed API is first introduced) and also some higher bound (as incompatible changes are so often). How do we formalize it? Well, let's use some mathematics and describe dependencies as interval! As a result a dependency on any compatible version 1.4.3 and later, would be written as 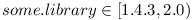some.library \in [ 1.4.3, 2.0).

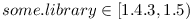This looks like a very good solution. It is also very rationalistic. It is reusing knowledge gained by mathematics in past and thus it cannot be wrong! Moreover it is general enough - one can use the same notation to express equality dependency by writing some.library \in [1.4.3, 1.4.3]. And also it is flexible as one can also depend on a smaller range of versions some.library \in [1.4.3, 1.5). Last, but not least this solution also supports some level of cluelessness as it builds on something every programmer must have heard of at own school days.

No wonder that everyone one who wants to be seen as providing well designed, deeply thought out, powerful and theoretically backed solution will choose intervals. This is probably the reason why OSGi decided to use this kind of dependencies.


Too Much Flexibility will Kill You!

Although it may seem flexible, improperly using RangeDependencies may lead to system that is too complex and almost no longer manageable. What traditionally happens only when people release incompatible versions (due to TransitivityOfIncompatibleChange) can suddenly happen in regular situations.

The proof claiming that managing module dependencies is NP-Complete operates with three types of modules:

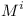  1. Mi which is present in two incompatible versions
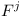  2. Fj which is present in three compatible versions
  3. a single module T

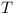
The claim is made that finding whether module 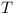T can be enabled is NP-Complete.

One of the most profound critiques however argues that it is wrong if three compatible versions of module 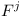Fj depend on incompatible versions of some other modules. This is valid observation, yet one can easily address it using RangeDependencies!

  1. instead of two incompatible versions of 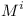Mi define two compatible versions: 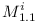M^i_{1.1} and M^i_{1.2}
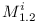
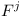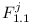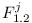  2. use strict range for dependencies of Fj, so F^j_{1.1} depends on M^i \in [1.1, 1.1] or F^j_{1.2} depends on M^i \in [1.2, 1.2]
  3. single module 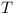T continue to depend on classical range of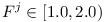 F^j \in [1.0, 2.0)

This scenario describes accepted practices of DistributedDevelopment. Imagine, there is one team providing various versions of module 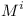Mi. This team does its best to keep BackwardCompatibility. It is using versioning in the traditional way to denote compatible versions - e.g. the first major number stays the same, the second minor one is incremented with each new, compatible version.

Yet there is some other distant team producing module(s) 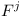Fj and this team (or its quality department) is afraid of signing blank checks and trusting the M-team to produce compatible versions. Thus they use restricted RangeDependency to require just subset of the versions (only those known during testing).

This is all that needs to happen. No incompatibilities, just a simple use of RangeDependencies and we are now facing an NP-Complete problem. This probably explains why there is 3SAT solver behind Equinox. Finding the right setup of modules depending on each other with RangeDependencies can be really hard. NP-Completely hard.

Retrieved from "http://wiki.apidesign.org/wiki/RangeDependencies"
Personal tools
buy