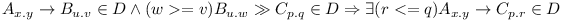LibraryWithoutImplicitExportIsPolynomial
From APIDesign
(→Module Dependency Proof No Longer Possible) |
(→Can we live with Complete Repositories?) |
||
| (20 intermediate revisions not shown.) | |||
| Line 1: | Line 1: | ||
| + | <skin>monobook</skin> | ||
| + | |||
The [[LibraryReExportIsNPComplete]] outlined the problem one has to face when practicing [[DistributedDevelopment]]. The [[LibraryReExportIsNPComplete|page]] also proved that in its global scope the problem is [[NP-Complete]] as any [[3SAT]] problem can be transformed to it. | The [[LibraryReExportIsNPComplete]] outlined the problem one has to face when practicing [[DistributedDevelopment]]. The [[LibraryReExportIsNPComplete|page]] also proved that in its global scope the problem is [[NP-Complete]] as any [[3SAT]] problem can be transformed to it. | ||
| - | The page also enumerated [[LibraryReExportIsNPComplete#Implications|implications]] associated with the [[NP-Complete]] nature of the problem and suggested that one way to eliminate them is to code in [[BackwardCompatibility|backward compatible]] way. However that is not always possible. | + | The page also enumerated [[LibraryReExportIsNPComplete#Implications|implications]] associated with the [[NP-Complete]] nature of the problem and suggested that one way to eliminate them is to code in [[BackwardCompatibility|backward compatible]] way. However that is not always possible. Another way to deal with the problem was to prevent re-exports. This is however even harder (imagine coding without the possibility to expose ''java.lang.String''). |
Surprisingly there seems to be an easy cure that eliminates the [[NP-Complete]] nature of the [[LibraryReExportIsNPComplete|library re-export]]. This page describes it in detail. | Surprisingly there seems to be an easy cure that eliminates the [[NP-Complete]] nature of the [[LibraryReExportIsNPComplete|library re-export]]. This page describes it in detail. | ||
| Line 10: | Line 12: | ||
A repository <math>R=(M,D)</math> is said to be ''complete'' if '''the transitive dependencies are explicitly enumerated''': | A repository <math>R=(M,D)</math> is said to be ''complete'' if '''the transitive dependencies are explicitly enumerated''': | ||
| - | # <math>A_{x.y} \rightarrow B_{u.v} \in D \wedge \exist w >= v B_{u.w} \gg C_{p.q} \in D \Rightarrow \exists r <= q A_{x.y} \rightarrow C_{p.r} \in D</math> | + | # <math>A_{x.y} \rightarrow B_{u.v} \in D \wedge \exist (w >= v) B_{u.w} \gg C_{p.q} \in D \Rightarrow \exists (r <= q) A_{x.y} \rightarrow C_{p.r} \in D</math> |
In the above the symbol <math>\rightarrow</math> may mean dependency with re-export (e.g. <math>\gg</math>) or dependency without re-export (e.g. <math>></math>). | In the above the symbol <math>\rightarrow</math> may mean dependency with re-export (e.g. <math>\gg</math>) or dependency without re-export (e.g. <math>></math>). | ||
| Line 21: | Line 23: | ||
== Polynomial == | == Polynomial == | ||
| - | Time to ask whether the problem remains [[NP-Complete]] or whether it enters the polynomial time complexity? Essential property of [[NP-Complete]] problems is that while finding | + | Time to ask whether the problem remains [[NP-Complete]] or whether it enters the polynomial time complexity? Essential property of [[NP-Complete]] problems is that while finding their solution requires a lot of time, verifying whether a solution is correct can be done in polynomial time. However that is what the ''complete repository'' does. Whenever we select a module, we also get all its necessary dependencies - we get a solution (in constant time, no need to seek for it) telling us what modules need to be enabled to enable the module on the top. If the ''complete repository'' is consistent, then we need to enable just those modules and we have a solution. |
| - | Thus the [[LibraryReExportIsNPComplete#Module Dependency Problem]] is solvable in polynomial time in ''complete repositories''. | + | Thus the [[LibraryReExportIsNPComplete#Module Dependency Problem|Module Dependency Problem]] is solvable in polynomial time in ''complete repositories''. |
== Consistency == | == Consistency == | ||
| Line 29: | Line 31: | ||
Next question is how complex it is to verify that a repository is ''complete repository''. We would not simplify our life if such a check was [[NP-Complete]]. In such case we would just trade one [[NP-Complete]] problem for another. But verifying that a repository is ''complete repository'' does not seem to be hard (e.g. it is polynomial). | Next question is how complex it is to verify that a repository is ''complete repository''. We would not simplify our life if such a check was [[NP-Complete]]. In such case we would just trade one [[NP-Complete]] problem for another. But verifying that a repository is ''complete repository'' does not seem to be hard (e.g. it is polynomial). | ||
| + | First thing to watch for is whether all transitive re-export dependencies are also expressed directly. That is obviously polynomial. | ||
| + | |||
| + | Second thing to check is whether all dependencies remain on compatible versions. Easy again. Just check if there is <math>A_{x.y} \rightarrow B{p.q} \in D \wedge A_{x.y} \rightarrow B{u.v} \in D \wedge p \neq u</math>. If there is such dependency, then the repository is inconsistent. Again, this is obviously polynomial problem. | ||
| + | |||
| + | == Can we live with Complete Repositories? == | ||
| + | |||
| + | Some may say that ''complete repositories'' are not practical and they are hard to maintain. This may be correct when it is not easy to identify that one reuses a feature re-exported by some module. For example in case of [[Functional compatibility]] one can depend on behaviour of a deeply hidden module (which is re-exported without direct dependency) and this is hard to identify. | ||
| + | |||
| + | On the other hand, there are other kind of [[BackwardCompatibility]] where ''complete repositories'' are natural. During compilation one needs all the module [[JAR]]s or header files to be present, not just those that one directly depends on. Even if one includes just '''java.applet''' module (in the proposed [[Modular Java SE]]), one also needs '''java.awt''' because the [http://java.sun.com/javase/6/docs/api/java/applet/Applet.html Applet] class extends (e.g. re-exports) classes from the '''java.awt''' module. The same applies to [[C]]'s use of ''stdio.h'' - it also needs bunch of other include files. | ||
| + | |||
| + | During compilation of our module, all these (re-exported) modules need to be present at certain version. It is enough to either enforce all these dependencies to be specified in order to compile (actually this is what [[Java]] compiler does, it does not allow you to compile against ''java-applet.jar'' and subclass the [http://java.sun.com/javase/6/docs/api/java/applet/Applet.html Applet] unless you also provide ''java-awt.jar'' on the classpath), or infer them by the compiler. Anyway it is clear that compilation is a natural moment when one can record (or generate) complete dependencies (so the module can be included in ''complete repository'') for just built module. | ||
| + | |||
| + | As the compilation is closely tight to linkage (and ability to link defines [[BinaryCompatibility]]), it is easy to generate ''complete repository'' of modules that can later be easily assembled and linked for execution in polynomial time. | ||
| + | |||
| + | == Merge of Configurations == | ||
| + | |||
| + | One additional issue needs consideration. When starting a system, one often needs to enable more than a single module. Some [[module system]]s provide good enough isolation, so running modules can use incompatible versions safely. However some systems require that each module is present in just a single version. The question then is: Is it easy to find out whether a set of modules can be enabled together (while only a single version of a module is present)? | ||
| + | |||
| + | Each module is equipped with a configuration (created during compilation). So the problem of enabling more modules reduces to a question whether, given a set of configurations one can find one which satisfies dependencies of all modules. This would be [[NP-Complete]] in common module repository, but in ''complete repositories'' this is a polynomial problem. | ||
| + | |||
| + | Just visit all the dependencies of all modules and if there is a dependency on module <math>A_{x.y}</math> and <math>A_{p.q}</math>, then: | ||
| + | # '''choose most recent version''': if <math>x = p</math> keep just <math>A_{x.max(q, y)}</math> | ||
| + | # '''detect incompatibilities''': if <math>x \neq p</math> then give up | ||
| + | |||
| + | The complexity of the above algorithm is polynomial. The fact that configuration produced by it satisfies all the module dependencies is obvious. The proof that if the algorithm gives up, there is no configuration in the ''complete repository'' to satisfy all the modules dependencies is left for reader's consideration. | ||
| + | |||
| + | == Making Compilation [[NP-Complete]]? == | ||
| + | |||
| + | Recent review of [[LibraryWithoutImplicitExportIsPolynomial|this proof]] raised an interesting question: Does not the suggestion to generate set of module's transitive [[dependencies]] at compile time mean | ||
| + | that you'd still have to run a general - and possibly [[NP-Complete]] - resolution algorithm at compile time in order to compute that set? | ||
| + | |||
| + | The [[NP-Complete|NP-Complexity]] during compilation seems to be avoided as the compilation is always done from bottom to top. As such we should be able to apply concept of [[wikipedia:Mathematical_induction|mathematical induction]]: | ||
| + | |||
| + | # '''module without dependencies''' - in almost any system there is at least one ''base'' module that does not have any dependencies. Computing set of dependencies of such module during compilation is obviously a constant operation. | ||
| + | # when '''compiling a module <math>M</math>''' with direct dependencies on <math>M_1, ..., M_n</math>. We can assume that <math>M_1, ..., M_n</math> have all their transitive dependencies explicitly enumerated (otherwise they could not be part of the ''complete repository''). Let's now collect all transitive dependencies of <math>M_1, ..., M_n</math> into a set and verify whether they are all consistent. This has already been explorered in [[#Merge of Configurations|merge of configurations]] section and is known to be polynomial. | ||
| + | |||
| + | In case the merged configuration of <math>M_1, ..., M_n</math> are consistent, we have new, polynomially sized (at most n times maximal size of configuration of individual module) configuration for module <math>M</math>. If the merged configuration is not consistent, the compilation should fail (in polynomial time) and the module <math>M</math> should not be created at all. As a result the [[NP-Complete]] threat is eliminated during compilation. | ||
| + | |||
| + | == Conclusion == | ||
| + | The way to fight with [[NP-Complete]] nature of [[LibraryReExportIsNPComplete|Module Dependency Problem]] is to generate ''complete repositories''. It is easy to create such repositories when one is primarily interested in coherent linkage of modules. All that is necessary is to modify our compilers to require (or infer and record) properly specified dependencies on all re-exported modules one is using, not just on the top level module that re-exports them. | ||
| - | == | + | == External Links == |
| - | + | # Lambda the Ultimate [http://lambda-the-ultimate.org/node/3594 discussion] | |
Current revision
The LibraryReExportIsNPComplete outlined the problem one has to face when practicing DistributedDevelopment. The page also proved that in its global scope the problem is NP-Complete as any 3SAT problem can be transformed to it.
The page also enumerated implications associated with the NP-Complete nature of the problem and suggested that one way to eliminate them is to code in backward compatible way. However that is not always possible. Another way to deal with the problem was to prevent re-exports. This is however even harder (imagine coding without the possibility to expose java.lang.String).
Surprisingly there seems to be an easy cure that eliminates the NP-Complete nature of the library re-export. This page describes it in detail.
Contents |
Library Versioning Terminology II
In addition to already existing terminology, let's define new type of repository:
A repository 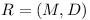R = (M,D) is said to be complete if the transitive dependencies are explicitly enumerated:
In the above the symbol 
may mean dependency with re-export (e.g.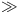 
) or dependency without re-export (e.g. > ).
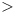The complete repository differs from the ordinary repository in the fact that there are no implicit re-export dependencies. Re-export itself is still possible, but it is required for each module to enumerate dependencies on each re-exported module it sees (or at least uses). Moreover such dependency needs to be compatible with the dependency of the re-exporting module (thus the p remains the same only r and q can differ).
Module Dependency Proof No Longer Possible
The first observation we shall notice is that it is not possible to reuse the proof described at LibraryReExportIsNPComplete on complete repositories. The essential part of the proof relies on the fact that the main module 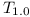T1.0 has dependencies only on modules 
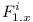. There were no restrictions of dependencies on modules 
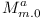. This will no longer be possible in complete repositories and as a result we don't have a proof that module dependency problem would be NP-Complete on complete repositories.
Polynomial
Time to ask whether the problem remains NP-Complete or whether it enters the polynomial time complexity? Essential property of NP-Complete problems is that while finding their solution requires a lot of time, verifying whether a solution is correct can be done in polynomial time. However that is what the complete repository does. Whenever we select a module, we also get all its necessary dependencies - we get a solution (in constant time, no need to seek for it) telling us what modules need to be enabled to enable the module on the top. If the complete repository is consistent, then we need to enable just those modules and we have a solution.
Thus the Module Dependency Problem is solvable in polynomial time in complete repositories.
Consistency
Next question is how complex it is to verify that a repository is complete repository. We would not simplify our life if such a check was NP-Complete. In such case we would just trade one NP-Complete problem for another. But verifying that a repository is complete repository does not seem to be hard (e.g. it is polynomial).
First thing to watch for is whether all transitive re-export dependencies are also expressed directly. That is obviously polynomial.
Second thing to check is whether all dependencies remain on compatible versions. Easy again. Just check if there is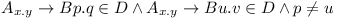 
. If there is such dependency, then the repository is inconsistent. Again, this is obviously polynomial problem.
Can we live with Complete Repositories?
Some may say that complete repositories are not practical and they are hard to maintain. This may be correct when it is not easy to identify that one reuses a feature re-exported by some module. For example in case of Functional compatibility one can depend on behaviour of a deeply hidden module (which is re-exported without direct dependency) and this is hard to identify.
On the other hand, there are other kind of BackwardCompatibility where complete repositories are natural. During compilation one needs all the module JARs or header files to be present, not just those that one directly depends on. Even if one includes just java.applet module (in the proposed Modular Java SE), one also needs java.awt because the Applet class extends (e.g. re-exports) classes from the java.awt module. The same applies to C's use of stdio.h - it also needs bunch of other include files.
During compilation of our module, all these (re-exported) modules need to be present at certain version. It is enough to either enforce all these dependencies to be specified in order to compile (actually this is what Java compiler does, it does not allow you to compile against java-applet.jar and subclass the Applet unless you also provide java-awt.jar on the classpath), or infer them by the compiler. Anyway it is clear that compilation is a natural moment when one can record (or generate) complete dependencies (so the module can be included in complete repository) for just built module.
As the compilation is closely tight to linkage (and ability to link defines BinaryCompatibility), it is easy to generate complete repository of modules that can later be easily assembled and linked for execution in polynomial time.
Merge of Configurations
One additional issue needs consideration. When starting a system, one often needs to enable more than a single module. Some module systems provide good enough isolation, so running modules can use incompatible versions safely. However some systems require that each module is present in just a single version. The question then is: Is it easy to find out whether a set of modules can be enabled together (while only a single version of a module is present)?
Each module is equipped with a configuration (created during compilation). So the problem of enabling more modules reduces to a question whether, given a set of configurations one can find one which satisfies dependencies of all modules. This would be NP-Complete in common module repository, but in complete repositories this is a polynomial problem.
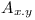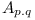Just visit all the dependencies of all modules and if there is a dependency on module Ax.y and Ap.q, then:
- choose most recent version: if 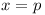x = p keep just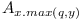 Ax.max(q,y)
- detect incompatibilities: if
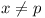then give up
The complexity of the above algorithm is polynomial. The fact that configuration produced by it satisfies all the module dependencies is obvious. The proof that if the algorithm gives up, there is no configuration in the complete repository to satisfy all the modules dependencies is left for reader's consideration.
Making Compilation NP-Complete?
Recent review of this proof raised an interesting question: Does not the suggestion to generate set of module's transitive dependencies at compile time mean that you'd still have to run a general - and possibly NP-Complete - resolution algorithm at compile time in order to compute that set?
The NP-Complexity during compilation seems to be avoided as the compilation is always done from bottom to top. As such we should be able to apply concept of mathematical induction:
- module without dependencies - in almost any system there is at least one base module that does not have any dependencies. Computing set of dependencies of such module during compilation is obviously a constant operation.
- when compiling a module 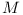M with direct dependencies on 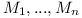M1,...,Mn. We can assume that 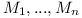M1,...,Mn have all their transitive dependencies explicitly enumerated (otherwise they could not be part of the complete repository). Let's now collect all transitive dependencies of 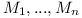M1,...,Mn into a set and verify whether they are all consistent. This has already been explorered in merge of configurations section and is known to be polynomial.
In case the merged configuration of 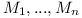M1,...,Mn are consistent, we have new, polynomially sized (at most n times maximal size of configuration of individual module) configuration for module 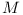M. If the merged configuration is not consistent, the compilation should fail (in polynomial time) and the module 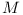M should not be created at all. As a result the NP-Complete threat is eliminated during compilation.
Conclusion
The way to fight with NP-Complete nature of Module Dependency Problem is to generate complete repositories. It is easy to create such repositories when one is primarily interested in coherent linkage of modules. All that is necessary is to modify our compilers to require (or infer and record) properly specified dependencies on all re-exported modules one is using, not just on the top level module that re-exports them.
External Links
- Lambda the Ultimate discussion
