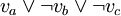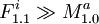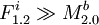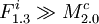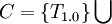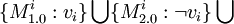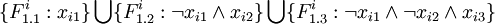LibraryReExportIsNPComplete
From APIDesign
Reusing libraries produced by others is essential aspect of DistributedDevelopment. It simplifies Time To Market, it reduces long term cost of ownership and leads to creation of good technologies. However it does not come for free. Read details or directly jump to the implications that shall improve your every day development habits.
This page starts by describing a way to convert any 3SAT problem to a solution of finding whether there is a way to satisfy all dependencies of a library in a repository of libraries. Thus proving that the later problem is NP-Complete. Then it describes the importance of such observations on our development practices.
There are similar observations for other module systems (RPM and Debian, see the external references section), with almost identical proof. The only difference is that both RPM and Debian allow easy way to specify negation by use of obsolete directive (thus it is easy to map the 3SAT formula). The unique feature of this proof is that it does not need negation at all. Instead it deals with re-export of an API. As re-export of APIs is quite common in software development, it brings implications of this kind of problem closer to reality.
Contents |
3SAT
The problem of satisfying a logic formula remains NP-complete even if all expressions are written in wikipedia::conjunctive normal form with 3 variables per clause (3-CNF), yielding the 3SAT problem. This means the expression has the form:
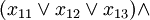
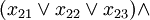
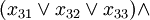
- ...
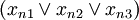
where each xab is a variable vi or a negation of a variable 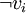 . Each variable vi can appear multiple times in the expression.
. Each variable vi can appear multiple times in the expression.
Library Versioning Terminology
Let A,B,C,... denote various modules and their APIs.
Let A1.0,A1.1,A1.7,A1.11 denote compatible versions of module A.
Let A1.0,A2.0,A3.1 denote incompatible versions of module A.
Let Ax.y > Bu.v denote the fact that version x.y of module A depends on version u.v of module B.
Let 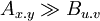 denote the fact that version x.y of module A depends on version u.v of module B and that it re-exports module B's API to users of own API.
denote the fact that version x.y of module A depends on version u.v of module B and that it re-exports module B's API to users of own API.
Let Repository R = (M,D) be any set of modules with their various versions and their dependencies on other modules with or without re-export.
Let C be a Configuration in a repository R = (M,D), if
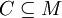 , where following is satisfied:
, where following is satisfied:
- re-exported dependency is satisfied with some compatible version:
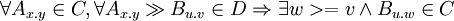
- each dependency is satisfied with some compatible version:
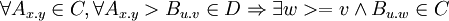
- each imported object has just one meaning for each importer: Let there be two chains of re-exported dependencies
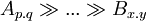 and
and 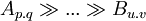 then
then 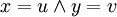
Module Dependency Problem
Let there be a repository R = (M,D) and a module 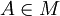 . Does there exist a configuration C in the repository R, such that the module
. Does there exist a configuration C in the repository R, such that the module 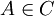 , e.g. the module can be enabled?
, e.g. the module can be enabled?
Conversion of 3SAT to Module Dependencies Problem
Let there be 3SAT formula with with variables v1,...,vm as defined above.
Let's create a repository of modules R. For each variable vi let's create two modules 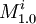 and
and 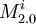 , which are mutually incompatible and put them into repository R.
, which are mutually incompatible and put them into repository R.
For each formula
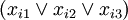 let's create a module Fi that will have three compatible versions. Each of them will depend on one variable's module. In case the variable is used with negation, it will depend on version 2.0, otherwise on version 1.0. So for formula
let's create a module Fi that will have three compatible versions. Each of them will depend on one variable's module. In case the variable is used with negation, it will depend on version 2.0, otherwise on version 1.0. So for formula
we will get:
All these modules and dependencies are added into repository R
Now we will create a module T1.0 that depends on all formulas:
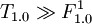
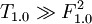
- ...
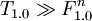
and add this module as well as its dependencies into repository R.
Claim: There 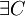 (a configuration) of repository R and
(a configuration) of repository R and 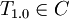
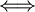 there is a solution to the 3SAT formula.
there is a solution to the 3SAT formula.
Proof
"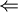 ": Let's have an evaluation of each variable to either true or false that evaluates the whole 3SAT formula to true. Then
": Let's have an evaluation of each variable to either true or false that evaluates the whole 3SAT formula to true. Then
It is clear from the definition that each Mi and Fi can be in the C just in one version. Now it is important to ensure that each module is present always at least in one version. This is easy for Mi as its vi needs to be true or false, and that means one of 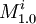 or
or 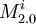 will be included. Can there be a Fi which is not included? Only if
will be included. Can there be a Fi which is not included? Only if 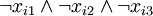 but that would mean the whole 3-or would evaluate to false and as a result also the 3SAT formula would evaluate to false. This means that dependencies of T1.0 on Fi modules are satisfied. Are also dependencies of every
but that would mean the whole 3-or would evaluate to false and as a result also the 3SAT formula would evaluate to false. This means that dependencies of T1.0 on Fi modules are satisfied. Are also dependencies of every 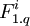 satisfied? From all the three versions, there is just one
satisfied? From all the three versions, there is just one 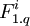 , the one its xiq evaluates to true. However xiq can either be without negation, and as such
, the one its xiq evaluates to true. However xiq can either be without negation, and as such 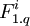 depends on
depends on 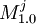 which is included as vj is true. Or xiq contains negation, and as such
which is included as vj is true. Or xiq contains negation, and as such 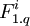 depends on
depends on 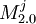 which is included as vj is false.
which is included as vj is false.
"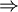 ": Let's have a C configuration satisfies all dependencies of T1.0. Can we also find positive valuation of 3SAT formula?
": Let's have a C configuration satisfies all dependencies of T1.0. Can we also find positive valuation of 3SAT formula?
For i-th 3-or there is 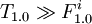 dependency which is satisfied. That means
dependency which is satisfied. That means 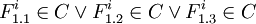 - at least one version of Fi module is present in the configuration. The one Fi that has the satisfied dependency reexports
- at least one version of Fi module is present in the configuration. The one Fi that has the satisfied dependency reexports 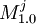 (which means vj = true) or
(which means vj = true) or 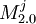 (which means vj = false). Anyway each i 3-or evaluates to true.
(which means vj = false). Anyway each i 3-or evaluates to true.
The only remaining question is whether a C configuration can force truth variable vj to be true in one 3-or and false in another. However that would mean that there is re-export via 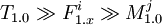 and also another one via
and also another one via 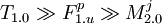 . However those two chain of dependencies ending in different versions of Mj cannot be in one C as that breaks the last condition of configuration definition (each imported object has just one meaning). Thus each Mj is represented only by one version and each vj is evaluated either to true or false, but never both.
. However those two chain of dependencies ending in different versions of Mj cannot be in one C as that breaks the last condition of configuration definition (each imported object has just one meaning). Thus each Mj is represented only by one version and each vj is evaluated either to true or false, but never both.
The 3SAT formula's evaluation based on the configuration C is consistent and satisfies the formula.
qed.
Polemics
One of the critiques raised during the LtU review (linked in external sources) is that the kind of situation cannot happen in practise. Surprisingly it can. OSGi and its RangeDependencies lead naturally into NP-Complete problems. Read more...
Implications
If there is a repository of modules in various (incompatible) versions, with mutual dependencies and re-export of their APIs, then deciding whether some of them can be enabled is NP-complete problem.
As NP-complete problems are hard to solve, it is usually our best desire to avoid them in real life situations. What does that mean in case one decides to practise DistributedDevelopment (and it is inevitable that software for 21st century needs this development style)? If you want to avoid headaches with finding the right configuration of various version of the libraries that allows to execute them together, then stick with following simple rules.
Be Compatible!
If you develop your own libraries in backward compatible way, you can always select the most recent version of each library. That is the configuration you are looking for. It is easy to find (obviously) and also it is the most desirable, as it delivers the most modern features and bugfixes that users of such libraries want.
Reuse with Care!
If you happen to reuse libraries (and you should because reuse lowers Time To Market, just like it did for me when I was publishing my first animated movie), then choose such libraries that can be trusted to evolve compatibly.
Hide Incompatibilities!
If you happen to reuse a library that cannot be trusted to keep its BackwardCompatibility, then do whatever you can to not re-export its APIs! This has been discussed in Chapter 10, Cooperating with Other APIs, but in short: If you hide such library for internal use and do not export any of its interfaces, you can use whatever version of library you want (even few years older) and nobody shall notice. Moreover in many module systems there can even be multiple versions of the same library in case they are not re-exported.
Explicit Re-export
Looks like there is a way to eliminate the NP-Completeness by disabling implicit re-export. See LibraryWithoutImplicitExportIsPolynomial. However this works only in a system with standardized versioning policy and without use of RangeDependencies.
Conclusion
Avoid complexities and NP-complete problems. Learn to develop in backward compatible way. Reading TheAPIBook is a perfect entry point into such compatible software design of the 21st century.
External Links
- discussion at Lambda the Ultimate
- LtU guys pointed out that the proof has already been published: D. Burrows, Modelling and Resolving Software Dependencies
- Equinox is said to use SAT4J solver
- EDOS Project seems to find similar proof: See section 3.2 in edos-wp2d1.pdf