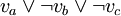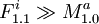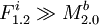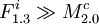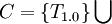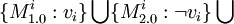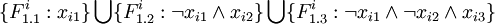LibraryReExportIsNPComplete
From APIDesign
(→Proof) |
|||
| Line 1: | Line 1: | ||
| - | This page describes a way to convert any [[ | + | This page describes a way to convert any [[3SAT]] problem to a solution of finding the right configuration from conflicting libraries in a system that can re-export APIs. Thus proving that the later problem is [[wikipedia::NP-complete]]. |
| - | == [[ | + | == [[3SAT]] == |
The problem of satisfying a logic formula remains '''NP'''-complete even if all expressions are written in ''[[wikipedia::conjunctive normal form]]'' with 3 variables per clause (3-CNF), yielding the '''3SAT''' problem. This means the expression has the form: | The problem of satisfying a logic formula remains '''NP'''-complete even if all expressions are written in ''[[wikipedia::conjunctive normal form]]'' with 3 variables per clause (3-CNF), yielding the '''3SAT''' problem. This means the expression has the form: | ||
| Line 35: | Line 35: | ||
Let there be a repository <math>R=(M,D)</math> and a module <math>A \in M</math>. Does there exist a configuration <math>C</math> in the repository <math>R</math>, such that the module <math>A \in C</math>, e.g. the module can be enabled? | Let there be a repository <math>R=(M,D)</math> and a module <math>A \in M</math>. Does there exist a configuration <math>C</math> in the repository <math>R</math>, such that the module <math>A \in C</math>, e.g. the module can be enabled? | ||
| - | == Converstion of [[ | + | == Converstion of [[3SAT]] to Module Dependencies Problem == |
| - | Let there be [[ | + | Let there be [[3SAT]] formula with with variables <math>v_1, ..., v_m</math> as defined above. |
Let's create a repository of modules <math>R</math>. For each variable <math>v_i</math> let's create two modules <math>M^i_{1.0}</math> and <math>M^i_{2.0}</math>, which are mutually incompatible and put them into repository <math>R</math>. | Let's create a repository of modules <math>R</math>. For each variable <math>v_i</math> let's create two modules <math>M^i_{1.0}</math> and <math>M^i_{2.0}</math>, which are mutually incompatible and put them into repository <math>R</math>. | ||
| Line 58: | Line 58: | ||
and add this module as well as its dependencies into repository <math>R</math>. | and add this module as well as its dependencies into repository <math>R</math>. | ||
| - | '''Claim''': There <math>\exists C</math> (a configuration) of repository <math>R</math> and <math>T_{1.0} \in C</math> <math>\Longleftrightarrow</math> there is a solution to the [[ | + | '''Claim''': There <math>\exists C</math> (a configuration) of repository <math>R</math> and <math>T_{1.0} \in C</math> <math>\Longleftrightarrow</math> there is a solution to the [[3SAT]] formula. |
== Proof == | == Proof == | ||
| - | "<math>\Leftarrow</math>": Let's have an evaluation of each variable to either true or false that evaluates the whole [[ | + | "<math>\Leftarrow</math>": Let's have an evaluation of each variable to either true or false that evaluates the whole [[3SAT]] formula to true. Then |
:<math>C = \{ T_{1.0} \} \bigcup</math> | :<math>C = \{ T_{1.0} \} \bigcup</math> | ||
:<math>\{ M^i_{1.0} : v_i \} \bigcup \{M^i_{2.0} : \neg v_i \} \bigcup</math> | :<math>\{ M^i_{1.0} : v_i \} \bigcup \{M^i_{2.0} : \neg v_i \} \bigcup</math> | ||
:<math>\{ F^i_{1.1} : x_{i1} \} \bigcup \{ F^i_{1.2} : \neg x_{i1} \wedge x_{i2} \} \bigcup \{ F^i_{1.3} : \neg x_{i1} \wedge \neg x_{i2} \wedge x_{i3} \}</math> | :<math>\{ F^i_{1.1} : x_{i1} \} \bigcup \{ F^i_{1.2} : \neg x_{i1} \wedge x_{i2} \} \bigcup \{ F^i_{1.3} : \neg x_{i1} \wedge \neg x_{i2} \wedge x_{i3} \}</math> | ||
| - | It is clear from the definition that each <math>M^i</math> and <math>F^i</math> can be in the <math>C</math> just in one version. Now it is important to ensure that each module is present always at least in one version. This is easy for <math>M^i</math> as its <math>v_i</math> needs to be true or false, and that means one of <math>M^i_{1.0}</math> or <math>M^i_{2.0}</math> will be included. Can there be a <math>F^i</math> which is not included? Only if <math>\neg x_{i1} \wedge \neg x_{i2} \wedge \neg x_{i3}</math> but that would mean the whole ''3-or'' would evaluate to false and as a result also the [[ | + | It is clear from the definition that each <math>M^i</math> and <math>F^i</math> can be in the <math>C</math> just in one version. Now it is important to ensure that each module is present always at least in one version. This is easy for <math>M^i</math> as its <math>v_i</math> needs to be true or false, and that means one of <math>M^i_{1.0}</math> or <math>M^i_{2.0}</math> will be included. Can there be a <math>F^i</math> which is not included? Only if <math>\neg x_{i1} \wedge \neg x_{i2} \wedge \neg x_{i3}</math> but that would mean the whole ''3-or'' would evaluate to false and as a result also the [[3SAT]] formula would evaluate to false. This means that dependencies of <math>T_{1.0}</math> on <math>F^i</math> modules are satisfied. Are also dependencies of every <math>F^i_{1.q}</math> satisfied? From all the three versions, there is just one <math>F^i_{1.q}</math>, the one its <math>x_{iq}</math> evaluates to true. However <math>x_{iq}</math> can either be without negation, and as such <math>F^i_{1.q}</math> depends on <math>M^j_{1.0}</math> which is included as <math>v_j</math> is true. Or <math>x_{iq}</math> contains negation, and as such <math>F^i_{1.q}</math> depends on <math>M^j_{2.0}</math> which is included as <math>v_j</math> is false. '''qed'''. |
Revision as of 09:54, 11 February 2009
This page describes a way to convert any 3SAT problem to a solution of finding the right configuration from conflicting libraries in a system that can re-export APIs. Thus proving that the later problem is wikipedia::NP-complete.
Contents |
3SAT
The problem of satisfying a logic formula remains NP-complete even if all expressions are written in wikipedia::conjunctive normal form with 3 variables per clause (3-CNF), yielding the 3SAT problem. This means the expression has the form:
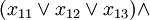
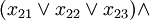
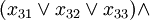
- ...
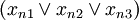
where each xab is a variable vi or a negation of a variable 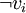 . Each variable vi can appear multiple times in the expression.
. Each variable vi can appear multiple times in the expression.
Module Dependencies Problem
Let A,B,C,... denote an API.
Let A1,A1.1,A1.7,A1.11 denote compatible versions of API A.
Let A1,A2.0,A3.1 denote incompatible versions of API A.
Let Ax.y > Bu.v denote the fact that version x.y of API A depends on version u.v of API B.
Let 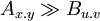 denote the fact that version x.y of API A depends on version u.v of API B and that it re-exports B's elements.
denote the fact that version x.y of API A depends on version u.v of API B and that it re-exports B's elements.
Let Repository R = (M,D) be any set of modules with their various versions and their dependencies on other modules with or without re-export.
Let C be a Configuration in a repository R = (M,D), if
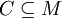 , where following is satisfied:
, where following is satisfied:
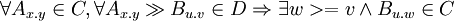 - each re-exported dependency is satisfied with some compatible version
- each re-exported dependency is satisfied with some compatible version
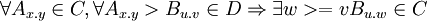 - each dependency is satisfied with some compatible version
- each dependency is satisfied with some compatible version
- Let there be two chains of re-exported dependencies
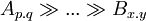 and
and 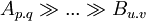 then
then 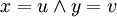 - this guarantees that each class has just one, exact meaning for each importer
- this guarantees that each class has just one, exact meaning for each importer
Module Dependency Problem
Let there be a repository R = (M,D) and a module 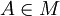 . Does there exist a configuration C in the repository R, such that the module
. Does there exist a configuration C in the repository R, such that the module 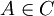 , e.g. the module can be enabled?
, e.g. the module can be enabled?
Converstion of 3SAT to Module Dependencies Problem
Let there be 3SAT formula with with variables v1,...,vm as defined above.
Let's create a repository of modules R. For each variable vi let's create two modules 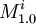 and
and 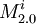 , which are mutually incompatible and put them into repository R.
, which are mutually incompatible and put them into repository R.
For each formula
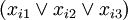 let's create a module Fi that will have three compatible versions. Each of them will depend on one variable's module. In case the variable is used with negation, it will depend on version 2.0, otherwise on version 1.0. So for the formula
let's create a module Fi that will have three compatible versions. Each of them will depend on one variable's module. In case the variable is used with negation, it will depend on version 2.0, otherwise on version 1.0. So for the formula
we will get:
All these modules and dependencies add into repository R
Now we will create a module T1.0 that depends all formulas:
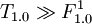
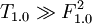
- ...
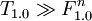
and add this module as well as its dependencies into repository R.
Claim: There 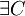 (a configuration) of repository R and
(a configuration) of repository R and 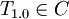
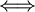 there is a solution to the 3SAT formula.
there is a solution to the 3SAT formula.
Proof
"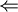 ": Let's have an evaluation of each variable to either true or false that evaluates the whole 3SAT formula to true. Then
": Let's have an evaluation of each variable to either true or false that evaluates the whole 3SAT formula to true. Then
It is clear from the definition that each Mi and Fi can be in the C just in one version. Now it is important to ensure that each module is present always at least in one version. This is easy for Mi as its vi needs to be true or false, and that means one of 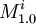 or
or 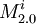 will be included. Can there be a Fi which is not included? Only if
will be included. Can there be a Fi which is not included? Only if 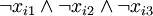 but that would mean the whole 3-or would evaluate to false and as a result also the 3SAT formula would evaluate to false. This means that dependencies of T1.0 on Fi modules are satisfied. Are also dependencies of every
but that would mean the whole 3-or would evaluate to false and as a result also the 3SAT formula would evaluate to false. This means that dependencies of T1.0 on Fi modules are satisfied. Are also dependencies of every 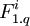 satisfied? From all the three versions, there is just one
satisfied? From all the three versions, there is just one 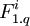 , the one its xiq evaluates to true. However xiq can either be without negation, and as such
, the one its xiq evaluates to true. However xiq can either be without negation, and as such 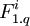 depends on
depends on 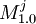 which is included as vj is true. Or xiq contains negation, and as such
which is included as vj is true. Or xiq contains negation, and as such 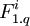 depends on
depends on 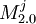 which is included as vj is false. qed.
which is included as vj is false. qed.