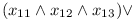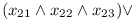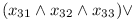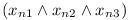LibraryReExportIsNPComplete

From APIDesign

This page describes a way to convert any wikipedia::3SAT problem to a solution of finding the right configuration from conflicting libraries in a system that can re-export APIs. Thus proving that the later problem is wikipedia::NP-complete.

wikipedia::3SAT

The problem of satisfying a logic formula remains NP-complete even if all expressions are written in wikipedia::conjunctive normal form with 3 variables per clause (3-CNF), yielding the 3SAT problem. This means the expression has the form:

Failed to parse (unknown error): (x_{11} \wedge x_{12} \wedge x_{13}) \vee

Failed to parse (unknown error): (x_{21} \wedge x_{22} \wedge x_{23}) \vee

Failed to parse (unknown error): (x_{31} \wedge x_{32} \wedge x_{33}) \vee

Failed to parse (unknown error): ...

Failed to parse (unknown error): (x_{n1} \wedge x_{n2} \wedge x_{n3})

where each 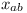Failed to parse (unknown error): x_{ab}

is a variable Failed to parse (unknown error): v_i
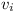or a negation of a variable Failed to parse (unknown error): \neg v_i

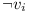. Each variable Failed to parse (unknown error): v_i

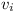can appear multiple times in the expression.

Module Dependencies Problem

Let 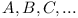Failed to parse (unknown error): A, B, C, ...

denote an API.

Let 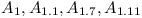Failed to parse (unknown error): A_1, A_{1.1}, A_{1.7}, A_{1.11}

denote compatible versions of API Failed to parse (unknown error): A

.

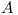Let 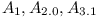Failed to parse (unknown error): A_1, A_{2.0}, A_{3.1}

denote incompatible versions of API Failed to parse (unknown error): A

.

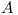Let 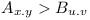Failed to parse (unknown error): A_{x.y} > B_{u.v}

denote the fact that version x.y of API A depends on version u.v of API B.

Let 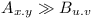Failed to parse (unknown error): A_{x.y} \gg B_{u.v}

denote the fact that version x.y of API A depends on version u.v of API B and that B re-exports its elements.

Let Repository 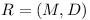Failed to parse (unknown error): R=(M,D)

be any set of modules with their various versions and their dependencies on other modules with or without re-export.

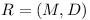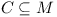Let C be a Configuration in a repository Failed to parse (unknown error): R=(M,D) , if Failed to parse (unknown error): C \subseteq M , where following is satisfied:

Failed to parse (unknown error): \forall A_{x.y} \in C, \forall A_{x.y} \gg B_{u.v} \in D \Rightarrow \exists w >= v \wedge B_{u.w} \in C

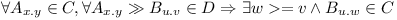- each re-exported dependency is satisfied with some compatible version

Failed to parse (unknown error): \forall A_{x.y} \in C, \forall A_{x.y} > B_{u.v} \in D \Rightarrow \exists w >= v B_{u.w} \in C

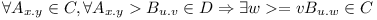- each dependency is satisfied with some compatible version

Let there be two chains of re-exported dependencies Failed to parse (unknown error): A_{p.q} \gg ... \gg B_{x.y}

and Failed to parse (unknown error): A_{p.q} \gg ... \gg B_{u.v}
then Failed to parse (unknown error): x = u \wedge y = v
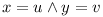- this guarantees that each class has just one, exact meaning for each importer

Module Dependency Problem: Let there be a repository 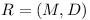Failed to parse (unknown error): R=(M,D)

and a module Failed to parse (unknown error): A \in M

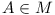. Does there exist a configuration Failed to parse (unknown error): C

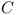in the repository Failed to parse (unknown error): R

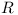, such that the module 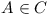Failed to parse (unknown error): A \in C , e.g. the module can be enabled?

Converstion of wikipedia::3SAT to Module Dependencies Problem

Let

Failed to parse (unknown error): (x_{11} \wedge x_{12} \wedge x_{13}) \vee

Failed to parse (unknown error): (x_{21} \wedge x_{22} \wedge x_{23}) \vee

Failed to parse (unknown error): (x_{31} \wedge x_{32} \wedge x_{33}) \vee

Failed to parse (unknown error): ...

Failed to parse (unknown error): (x_{n1} \wedge x_{n2} \wedge x_{n3})

be a formula with variables 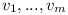Failed to parse (unknown error): v_1, ..., v_m .

For each variable 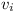Failed to parse (unknown error): v_i

let's create two modules Failed to parse (unknown error): M^i_{1.0}
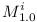and Failed to parse (unknown error): M^i_{2.0}

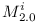, which are mutually incompatible.

For each formula let's create a module F that will have three compatible versions. Each of them will depend on one variable. In case the variable is used with negation, it will depend on version 2, otherwise on version 1. So for the formula (x_a or ¬x_b or ¬x_c) we will get: F_1.1[^A₁] and F_1.2[^B₂] and F_1.3[^C₂]

Now we will create a module M that depends all formulas: M[F_1.0, G_1.0, ...]. The claim is that iff there is a way to satisfy all dependencies of module M, then there is a solution to the wikipedia::3SAT formula.