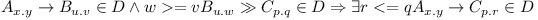LibraryWithoutImplicitExportIsPolynomial
From APIDesign
(→Polynomial) |
(→Consistency) |
||
| Line 29: | Line 29: | ||
Next question is how complex it is to verify that a repository is ''complete repository''. We would not simplify our life if such a check was [[NP-Complete]]. In such case we would just trade one [[NP-Complete]] problem for another. But verifying that a repository is ''complete repository'' does not seem to be hard (e.g. it is polynomial). | Next question is how complex it is to verify that a repository is ''complete repository''. We would not simplify our life if such a check was [[NP-Complete]]. In such case we would just trade one [[NP-Complete]] problem for another. But verifying that a repository is ''complete repository'' does not seem to be hard (e.g. it is polynomial). | ||
| + | First thing to watch for is whether all transitive re-export dependencies are also expressed directly. That is obviously polynomial. | ||
| + | Second thing to watch for is whether all dependencies remain on compatible versions. Easy again. Just check if there is <math>A_{x.y} \rightarrow B{p.q} \wedge A_{x.y} \rightarrow B{u.v} \wedge p <> u</math>. Again obviously polynomial. | ||
== Can we live with Complete Repositories == | == Can we live with Complete Repositories == | ||
Sure, at least for [[SourceCompatibility]] and [[BinaryCompatibility]]. | Sure, at least for [[SourceCompatibility]] and [[BinaryCompatibility]]. | ||
Revision as of 21:49, 1 September 2009
The LibraryReExportIsNPComplete outlined the problem one has to face when practicing DistributedDevelopment. The page also proved that in its global scope the problem is NP-Complete as any 3SAT problem can be transformed to it.
The page also enumerated implications associated with the NP-Complete nature of the problem and suggested that one way to eliminate them is to code in backward compatible way. However that is not always possible. The other suggested elimination of the problem was to prevent re-exports. This is however this is even harder (imagine coding without the possibility to expose java.lang.String).
Surprisingly there seems to be an easy cure that eliminates the NP-Complete nature of the library re-export. This page describes it in detail.
Contents |
Library Versioning Terminology II
In addition to already existing terminology, let's define new type of repository:
A repository 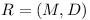 is said to be complete if the transitive dependencies are explicitly enumerated:
is said to be complete if the transitive dependencies are explicitly enumerated:
In the above the symbol  may mean dependency with re-export (e.g.
may mean dependency with re-export (e.g. 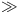 ) or dependency without re-export (e.g.
) or dependency without re-export (e.g. 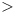 ).
).
The complete repository differs from the ordinary repository in the fact that there are no implicit re-export dependencies. Re-export itself is still possible, but it is required for each module to enumerate dependencies on each re-exported module it sees (or at least uses). Moreover such dependency needs to be compatible with the dependency of the re-exporting module (thus the p remains the same only r and q can differ).
Module Dependency Proof No Longer Possible
The first observation we shall notice is that it is not possible to reuse the proof described at LibraryReExportIsNPComplete on complete repositories. The essential part of the proof relies on the fact that the main module 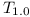 has dependencies only on modules
has dependencies only on modules 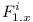 . There were no restrictions of dependencies on modules
. There were no restrictions of dependencies on modules 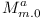 . This will no longer be possible in complete repositories and as a result we don't have a proof that module dependency problem would be NP-Complete on complete repositories.
. This will no longer be possible in complete repositories and as a result we don't have a proof that module dependency problem would be NP-Complete on complete repositories.
Polynomial
Time to ask whether the problem remains NP-Complete or whether it enters the polynomial time complexity? Essential property of NP-Complete problems is that while finding them requires a lot of time, verifying whether a solution is really a solution can be done in polynomial time. However that is what the complete repository does. Whenever we select a module, we also get all its necessary dependencies - we get a solution (in constant time, no need to seek for it) telling us what modules need to be enabled to enable the module on the top. If the complete repository is consistent, then we need to enable just those modules and we have a solution.
Thus the Module Dependency Problem is solvable in polynomial time in complete repositories.
Consistency
Next question is how complex it is to verify that a repository is complete repository. We would not simplify our life if such a check was NP-Complete. In such case we would just trade one NP-Complete problem for another. But verifying that a repository is complete repository does not seem to be hard (e.g. it is polynomial).
First thing to watch for is whether all transitive re-export dependencies are also expressed directly. That is obviously polynomial.
Second thing to watch for is whether all dependencies remain on compatible versions. Easy again. Just check if there is 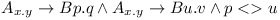 . Again obviously polynomial.
. Again obviously polynomial.
Can we live with Complete Repositories
Sure, at least for SourceCompatibility and BinaryCompatibility.