Talk:LibraryWithoutImplicitExportIsPolynomial
From APIDesign
| (One intermediate revision not shown.) | |||
| Line 6: | Line 6: | ||
Nice observation ;-) Probably I am disappointed by the enthusiasm followed by total failure of P == NP proof published by Vinay Deolalikar and thus I am assuming P != NP. | Nice observation ;-) Probably I am disappointed by the enthusiasm followed by total failure of P == NP proof published by Vinay Deolalikar and thus I am assuming P != NP. | ||
| + | |||
| + | Btw. now, when there is an expert reviewing my proof, I share my only worry: What if, in the process of replacing dependencies by transitive dependencies, the amount of dependencies is increased to <math>2^n</math>? That would just replace an [[NP-Complete]] problem with polynomial problem of exponential size... On the other hand, that is not likely, I guess as the transitive dependencies will contain only one version from multiple incompatible versions. | ||
--[[User:Apidesign|Apidesign]] 18:39, 25 December 2011 (UTC) | --[[User:Apidesign|Apidesign]] 18:39, 25 December 2011 (UTC) | ||
Current revision
A polynomial algorithm implies that the problem is not NP-Complete only if you assume that P != NP for which see P versus NP.
However, the important point that a known polynomial algorithm is more clearly bounded that a NP-Complete algorithm is fair enough.
-- A comment from unknown reader
Nice observation ;-) Probably I am disappointed by the enthusiasm followed by total failure of P == NP proof published by Vinay Deolalikar and thus I am assuming P != NP.
Btw. now, when there is an expert reviewing my proof, I share my only worry: What if, in the process of replacing dependencies by transitive dependencies, the amount of dependencies is increased to 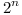2n? That would just replace an NP-Complete problem with polynomial problem of exponential size... On the other hand, that is not likely, I guess as the transitive dependencies will contain only one version from multiple incompatible versions.
--Apidesign 18:39, 25 December 2011 (UTC)
Follow
